Cluster World
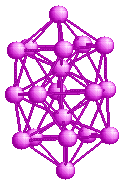
Structure of strontium clusters
Micro world is governed by atoms and molecules, and the macro world
consists of materials which contain a mind-boggling number of atoms or
molecules. For atoms and molecules we study chemistry - we talk of
chemical bonds, we talk of electronic orbitals, we talk of reactivity
of a molecule. In the macro-world we talk of properties like
electrical resistance, thermal conductivity, stiffness. We see distinct
phases of materials - liquid, solid and gas.
The bulk consists of atoms and molecules, so the properties of the
atoms and molecules should decide the properties of the bulk. This is a
challenging problem for scientists and only a little progress has been
made in this direction. One would like to see how things change as one
goes from atoms and molecules to small assemblies of them, to large
assemblies, to larger assemblies, and finally to the bulk. One would
like to see how various atoms, which do not appear very different
individually, work together to form metals, insulators and
semiconductors.
The study of clusters is aimed at looking at this
transition from the atomic state to the bulk.
How are small clusters made?
The most popular technique to produce atomic clusters is called the gas
aggregation technique. Here, a sample of the material whose clusters
are needed is heated in a furnace to such high temperatures that it
evaporates. In this vapour phase the material separates out into
individual atoms. This gas is mixed with a jet of some inert gas which
carries it forward. This inert gas is at low temperatures, and so the
atoms of the original material collide these and lose energy. Once they
lose energy, they can stick to each other better.
 So they start forming aggregates. The mass of these resulting clusters
is analyzed by a mass spectrometer.
So they start forming aggregates. The mass of these resulting clusters
is analyzed by a mass spectrometer.
It turns out that in this primeval soup of atoms, clusters of some size
are much more abundant than others. These clusters containing certain
special number of atoms seem to be much more stable compared to
others. These numbers are referred to as magic numbers. In this
primeval soup clusters collide with each other and lose atoms. So, only
the clusters which are more stable will be found to be abundant. Thus,
the magic numbers indicate the stability of certain clusters. The task
of a theoretian would be to explain this stability of some clusters,
or in other words, explain the magic numbers.
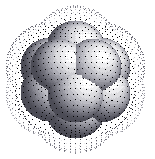
Magic numbers for rare-gases
The magic numbers seen for rare-gas clusters, like Argon,
Krypton, Neon are well understood. The magic numbers seen for these are
7, 13, 19, 23, 55. These numbers correspond to nice
close-packed structures which can be formed by packing spheres, as
shown below.



So, the special stability of rare-gas clusters is believed to be due
to this geometric close-packing of atoms in the clusters.
Magic numbers for metal clusters
The clusters of various metals were seen to show magic numbers which
are very different from that of rare-gases. Experiments were done on
Alkali metals like Lithium, Sodium, Potassium, and other metals like
Aluminium, which showed that the clusters are stable when the total number of free electrons in the cluster are 8, 20,
34, 40, 58, .... Notice that here the number of atoms in a
cluster is not important - what is important is the total number of
free electrons.
 This can be understood with the help of what is called the Jellium model. In the Jellium model, one assumes that
the outer electrons of the metal atoms are loosly bound so that when a
cluster is formed, they can move around everywhere in the clusters,
and are not bound to a particular atom. The atoms without their outer
electrons are positively charged ions. So, the free electrons "see" a
jellium of positive ions in the cluster. The electrons move around in
the positive jellium. If one tries to theoretically solve the problem
of free electrons in a positive jellium, one indeed observes that the
clusters are energetically most stable when the total number of
electrons in them are 8, 20, 34, 40, 58 etc! This simple picture can
be applied to many metals and works very well.
This can be understood with the help of what is called the Jellium model. In the Jellium model, one assumes that
the outer electrons of the metal atoms are loosly bound so that when a
cluster is formed, they can move around everywhere in the clusters,
and are not bound to a particular atom. The atoms without their outer
electrons are positively charged ions. So, the free electrons "see" a
jellium of positive ions in the cluster. The electrons move around in
the positive jellium. If one tries to theoretically solve the problem
of free electrons in a positive jellium, one indeed observes that the
clusters are energetically most stable when the total number of
electrons in them are 8, 20, 34, 40, 58 etc! This simple picture can
be applied to many metals and works very well.
Experiments on strontium clusters
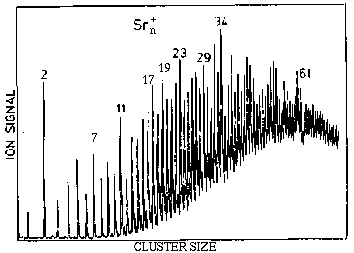 C. Brechignac and collaborators performed experiments on Sr clusters.
The "abundance spectrum" they obtained is shown in the figure.
Although strontium is a metal, it does not show magic numbers similar
to the Jellium model. One the other hand, the magic number seen are
closer to those for rare-gases. This is strange, because strontium
atoms cannot have a weak binding force as in rare-gases - so what is
the reason for this kind of magic numbers? Also, one would notice that
there is a magic number 11 which is not seen in rare-gases.
C. Brechignac and collaborators performed experiments on Sr clusters.
The "abundance spectrum" they obtained is shown in the figure.
Although strontium is a metal, it does not show magic numbers similar
to the Jellium model. One the other hand, the magic number seen are
closer to those for rare-gases. This is strange, because strontium
atoms cannot have a weak binding force as in rare-gases - so what is
the reason for this kind of magic numbers? Also, one would notice that
there is a magic number 11 which is not seen in rare-gases.
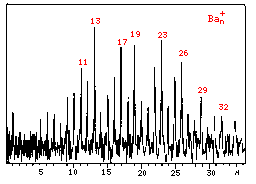 Let us have a look at the abundance spectra for Barium and Ytterbium.
Surprisingly, Ba and Yb also show magic numbers close
to those of rare-gases! So, what is common between these three
elements? Their electronic configuration looks like this:
Let us have a look at the abundance spectra for Barium and Ytterbium.
Surprisingly, Ba and Yb also show magic numbers close
to those of rare-gases! So, what is common between these three
elements? Their electronic configuration looks like this:
- Sr ------------ [Krypton] 5s2 4d0
- Ba ------------ [Xenon] 6s2 5d0
- Yb ------------ [Xenon] 4f14 6s2 5d0
All of these three elements have a ns2 "closed shell"
configuration, which means that to add one more electron to the atom, a
new shell has to be added. All of these also have the d-states as the
immediate next unoccupied states. It appears that this feature may
have something to do with the similar kind of magic numbers seen in
the clusters of these elements.
Car-Parrinello molecular dynamics simulation
Atoms which are not very light, are generally expected to behave like
classical particles. So, it makes sense to do a computer simulation of
clusters by letting the atoms evolve via Newton's equations of motion.
For this one just needs the knowledge of the initial position and
velocities of the atoms, and the forces between them. The calculation
of force between two atoms is a non-trivial job because this force has
its roots in the electronic structure of the atoms. The electronic
structure has to be treated quantum mechanically. This calculation is
tedious and can only be done approximately.
The tool one uses to calculate the electronic structure of the cluster
is the density functional theory introduced by Walter Kohn. Using this
one can calculate the ground state energy of the cluster. M.
Parrinello and R. Car came up with an innovative method which combines
the density functional calculation for electrons and classical
molecular dynamics for atoms, in a single unified formalism. This
method has come to be known as the Car-Parrinello molecular dynamics
(CPMD).
 ---Inclusion of d-electrons leads to---->
---Inclusion of d-electrons leads to---->

 This can be understood with the help of what is called the Jellium model. In the Jellium model, one assumes that
the outer electrons of the metal atoms are loosly bound so that when a
cluster is formed, they can move around everywhere in the clusters,
and are not bound to a particular atom. The atoms without their outer
electrons are positively charged ions. So, the free electrons "see" a
jellium of positive ions in the cluster. The electrons move around in
the positive jellium. If one tries to theoretically solve the problem
of free electrons in a positive jellium, one indeed observes that the
clusters are energetically most stable when the total number of
electrons in them are 8, 20, 34, 40, 58 etc! This simple picture can
be applied to many metals and works very well.
This can be understood with the help of what is called the Jellium model. In the Jellium model, one assumes that
the outer electrons of the metal atoms are loosly bound so that when a
cluster is formed, they can move around everywhere in the clusters,
and are not bound to a particular atom. The atoms without their outer
electrons are positively charged ions. So, the free electrons "see" a
jellium of positive ions in the cluster. The electrons move around in
the positive jellium. If one tries to theoretically solve the problem
of free electrons in a positive jellium, one indeed observes that the
clusters are energetically most stable when the total number of
electrons in them are 8, 20, 34, 40, 58 etc! This simple picture can
be applied to many metals and works very well.
 So they start forming aggregates. The mass of these resulting clusters
is analyzed by a mass spectrometer.
So they start forming aggregates. The mass of these resulting clusters
is analyzed by a mass spectrometer.


 C. Brechignac and collaborators performed experiments on Sr clusters.
The "abundance spectrum" they obtained is shown in the figure.
Although strontium is a metal, it does not show magic numbers similar
to the Jellium model. One the other hand, the magic number seen are
closer to those for rare-gases. This is strange, because strontium
atoms cannot have a weak binding force as in rare-gases - so what is
the reason for this kind of magic numbers? Also, one would notice that
there is a magic number 11 which is not seen in rare-gases.
C. Brechignac and collaborators performed experiments on Sr clusters.
The "abundance spectrum" they obtained is shown in the figure.
Although strontium is a metal, it does not show magic numbers similar
to the Jellium model. One the other hand, the magic number seen are
closer to those for rare-gases. This is strange, because strontium
atoms cannot have a weak binding force as in rare-gases - so what is
the reason for this kind of magic numbers? Also, one would notice that
there is a magic number 11 which is not seen in rare-gases.  Let us have a look at the abundance spectra for Barium and Ytterbium.
Surprisingly, Ba and Yb also show magic numbers close
to those of rare-gases! So, what is common between these three
elements? Their electronic configuration looks like this:
Let us have a look at the abundance spectra for Barium and Ytterbium.
Surprisingly, Ba and Yb also show magic numbers close
to those of rare-gases! So, what is common between these three
elements? Their electronic configuration looks like this: ---Inclusion of d-electrons leads to---->
---Inclusion of d-electrons leads to---->
