Quantum tunneling of Hydrogen in Niobium

Schematic picture of a Hydrogen atom (white), in BCC Niobium, tunneling between two energetically equivalent sites. These sites are low in energy because of the presence of the impurity atom Oxygen (red).

Trapping of H in Nb

Niobium (Nb) is a metal which is superconducting below a temperature of 9.2K. Nb has a body-centered-cubic (BCC) structure.

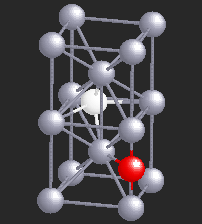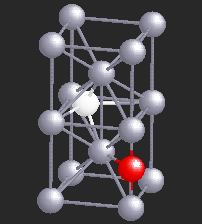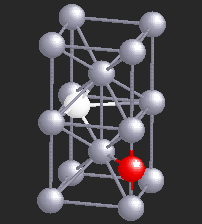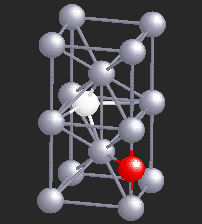
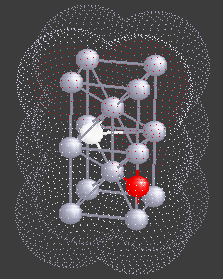
Hydrogen (H), being a small atom, if introduced in a Nb sample, can sit in the interstitial sites between the Nb atoms. At very low temperatures H is seen to move freely through the Nb lattice of atoms. However, if there are certain impurity atoms like Oxygen (O) or Nitrogen (N), present in the Nb sample, they form trapping centers for the otherwise freely moving hydrogen atoms. A typical location of an Oxygen atom in the Nb lattic is shown by in red in the figure.

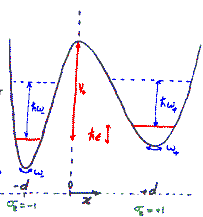
In the presence of Oxygen impurities, the H atom likes to stay around such impurity sites. It tries to sit at the site where its energy will be the lowest. It turns out that the two sites shown in the figure are the lowest energy sites for the H atom (shown in white). These sites are physically quite close, and also energetically identical for the H atom. The hydrogen atom near such sites "sees" a potential which is like a double-well. However, in a given sample of Nb, there are many such double-wells because there are many H atoms trapped around Oxygen impurities. The presence of other impurities affect the symmetry of the double-well, and it will in general be asymmetric, as shown in the figure below. It can stay in either of the two wells, but not in between. At high temperatures H atom has enough energy to jump the barrier between the two wells. At low temperatures it can stay in either of the two wells, but cannot jump from one to the other.

This is true for things which follow Newton's laws. But a hydrogen atom is too small to be contrained by Newton's laws. It takes advantage of the laws of the Qunatum theory, which is a more fundamental theory of nature, and is seen only when one goes to atomic scales. Even if the H atom doesn't have enough energy to jump over the barrier, it can grow fuzzy and just "tunnel" to the other site! Quantum mechanic allows this. Left to itself at a particular site, the H atom will execute a coherent clock like motion between the two sites. This is called "quantum tunneling".

Neutron-scattering experiments

This was observed in beautiful experiments by Helmut Wipf and collaborators at Grenoble, France (H. Wipf et al, Europhys. Lett. 4 (1987) 1379). In these experiments neutrons with known energy are thrown on a sample of Niobium containing some Oxygen impurities, in which Hydrogen has been introduced. After the neutrons scatter off the sample atoms, their energy gain/loss is measured.

There are basically three kinds of scattering of neutrons:

Elastic scattering: In this process there is no energy gain or loss in the scattered neutron. If neutron bumps into a rigid immobile atom, this is the kind of scattering that takes place.
Inelastic scattering: In this kind of scattering there is a gain or loss of discrete quanta of energy from the neutron. If the neutron comes across an atom which is executing a periodic oscillation, there is inelastic scattering.
Quasi-elastic scattering: In this kind of scattering there is loss or gain of energy in randomly varying amounts. If a neutron collides with an atom which is randomly moving around, there is quasi-elastic scattering.

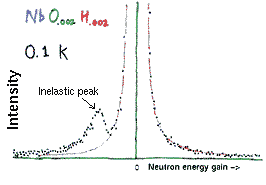
The energy gain/loss measured by Wipf and collaborators, at a temperature of 0.1K, is shown in the figure on the right. There is big peak at the center, which represents elastic scattering from immobile Nb atoms.

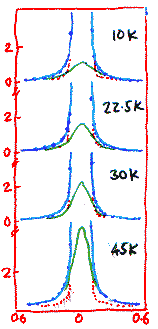
The quasi-elastic peak (shown in green) narrows down as the temperature is increased.

However, one can see a distinct inelastic peak at some discrete energy. This means there is an atom inside, which is executing a coherent clock-like motion! At this low temperature the H atom cannot jump the barrier between the two wells, so the only way it can move between the two sites is through tunneling. So, this experiment shows evidence for tunneling of H in Nb.

This, however, is just one part of the story. When the experiments were repeated at higher temperatures, inelastic scattering disappeared completely, and was replaced by a quasi-elastic peak. This, one would recall, indicates that the scattering atom is not moving coherently but incoherently. This means that the tunneling motion has been destroyed by something which is causing randomness.

The width of the quasi-elastic peak is supposed to quantify the rate at which the scattering atom is jumping randomly between two sites. Normally one expects that as the heat is turned on, the scattering atom is kicked around more and more and so the width of the quasi-elastic peak will increase with temperature. But here it was observed that the quasi-elastic peak actually narrows with the increasing temperature! This is really strange, for it means that as the temperature is increased, the atom tends to sit more on one site rather than jump around!

This is really weird - so let us try to see how this can happen. Recall that Nb is a metal. So the H atom which moves between the two sites, not only sees the double-well potential but also feels the effect of the sea of electrons formed by the outer electrons of Nb (see the picture alongside).

Each atom is surrounded by an electron "cloud", and in metals these clouds overlap so that there is a sea of electrons present throughout.

The electrons in Nb solid seem to have a drag on the moving H atom.

Effect of conduction electrons on tunneling of H

Effect of conduction electrons is not easy to study theoretically, as the problem involves studying so many particles all together. We simplified the problem to make it tractable. We approximate the tunneling H atom by a quantum two-level system. This two level system interacts with electrons, which are also treated approximately.

If one grinds through the calculation (S. Dattagupta and T. Qureshi, Physica B, 174 (1991) 262), one gets the following picture:

At very low temperatures, the effect of electrons is not destructive, and one observes coherent tunneling motion of H.
This tunneling frequency is highly suppressed because the motion of the H atom from one site to another requires the dragging of the surrounding electron cloud, together with it.
As the temperature is raised, the electrons destroy the coherent motion of H. Tunneling is possible still, but now it is incoherent, like random jumps.
The destruction of coherence lead to the H atom tending to sit on one site.
The frequency of jumps between the two sites is proportional to T^2K-1, where T is the temperature and K=0.055. This agrees with the experimental observation of decrease in the jump rate with increasing temperature.
This is an example of the "watched pot effect", which says that a watched pot never boils! It is also known as the Quantum Zeno effect. If one observes a quantum system, its time evolution is inhibited. In the limit of continuous observation, the system completely stops evolving and freezes in its initial state. Here the conduction electrons of the metal keep "watching" the H atom, and so it is not able to tunnel to the other site.