"Protective" measurements in quantum mechanics

Quantum mechanics is the most bizarre, and yet highly successful of the theories we know today. When applied to the physical world it comes out with flying colors. Yet the picture of reality which it leads to, is mind-boggling, to say the least. Einstein found the whole thing pretty hard to swallow and could not come to terms with it till the end of his life. In our familiar "classical" world, particles have well defined postions and momenta which are unique. Quantum mechanics on the other hand, allows for possibilities where the particle can be simultaneously "here" and also "there", so to speak. The idea can be best illustrated with the following example.

The Stern-Gerlach experiment

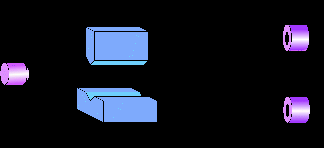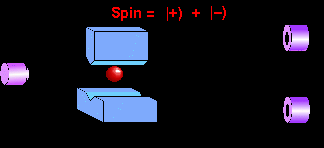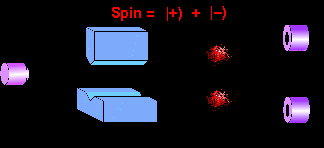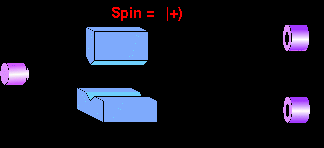This is a schematic representation of the classic Stern-Gerlach experiment with spin-half particles. A particle emerges from the source and travels towards the screen. The spin of the particle, at time t=0, is in a superposition state of pointing "up" (|+>) and pointing "down" (|->). It can be represented by

|t=0> = a|+> + b|->

As it passes through the magnets, the "up" component of the spin pulls the particle up, and the "down" component pulls it down. As a result, the particle becomes "fuzzy" and splits into a superposition of two wave-packets travelling in different directions. This is a bizarre state of the particle - it is simultaneously in two positions!

When this superpostion of wave-packets, on reaching the other end, interacts with the detectors, the quantum coherence is destroyed, and the particle is detected at one of the two positions. It will be detected up with a probability |a|² , and down with a probablity |b|² . We are back to the familiar classical world.

This last stage where the superposition of the two wave-packets is destroyed, and one ends up with a particle either "here" or "there", is loosely referred to as the wave function collapse.

For those who are not shocked by the above experiment, look at the case of the Schrodinger's Cat!

What is unknown, cannot be known!

As one might have guessed, after a measurement like the one made in the example described above, one doesn't acquire any information about the original state |t=0>. In a single measurement one either gets an "up" spin or a "down" spin - one doesn't know what original state led to the result obtained. And after one measurement, the state is irretrievably destroyed. So, any subsequent measurements too do not tell us anything about the original state. In effect, if the state is initially unknown, there is absolutely no way of knowing it! This is the generally accepted credo of quantum mechanics.

This scenario seems to indicate that the state, or the wavefunction, is not real - only if we possess sufficient knowledge about a system, we construct a wave-function for it. The fact that the only wave-functions we can measure are the ones already known to us, leads one to conclude that the wave-function is an entity which is formed out of our knowledge of the system - it doesn't have an independent existence. To put it in the philosophers jargon, the status of wave-function is "epistemological" (based on knowledge), and not "ontological" (real).

Can an unknown wave-function be "measured"?

Yakir Aharonov, Jeeva Anandan and Lev Vaidman came up with a scheme which they called "protective measurement", which is claimed to yield information about unknown wave-functions, although of a very special class. Let us try to understand what these protective measurements are.

Conventional measurement

Let us first see what happens in a conventional measurement, like the one in the SG experiment described above. Assume a particle of mass m, travelling along the x axis, a magnetic field along the z-axis, and that the field is inhomgeneous along the y-axis. Let the particle be in a wave-packet state centered around y=0, and can be respresented by the wavefunction f(0). Let the state of the spin be written as a|+>+b|->. The full wave-function of the particle at time t=0, when the particle just enters the region of the magnetic field, is thus written as |t=0> = ( a|+> + b|-> ) f(0) Let the magnetic field be of the form yB - then the Hamiltonian of the system is given by H = p²/2m + yB S_z where p the momentum of the particle along the y-axis and m is its mass. Then one can easily write the wave-function at time t=T as: |t=T> = e^iHT ( a|+> + b|-> ) f(0). One can assume that the particle is in the region of the magnetic field for a very short time, and the magnetic field is so strong that one can neglect the first term in the Hamiltonian. Then, |t=T> = e^{iyB S_zT} ( a|+> + b|-> ) f(0). We know that |+> and |-> are the eigenstates of S_z so that, S_z|+> = |+> and S_z|-> = -|->. Using this, one can write the above equation as: |t=T> = a|+>e^iyBTf(0) + b|->e^-iyBTf(0). Here e^iyBTf(0) and e^-iyBTf(0) represent two wave-packets evolving in two different dierections. Also, these wave-packets are correlated with the spin states |+> and |-> respectively. Such a state is called an entangled state. In this state, if one detects the position of the particle, one will get any one of the two wave-packets, and the spin state will "collapse" to the state correlated with that wave-packet. Thus we see that in a conventional measurement, the descruction of the initial state is inevitable because of the entanglement.

Protective measurement

Protective measurements are similar to conventional measurements except that they are weak and adiabatic (slow). But this makes the crucial difference as we will see now. Because the interaction is weak and acts for a long time, we cannot neglect the "free" Hamiltonian of the system and the apparatus. So the total Hamiltonian of the system-apparatus can be written as: H = p²/2m + g(t)p Q_s + H_s Here we assume that the interaction depends on p instead of the position of the particle. H_s is the Hamiltonian of the spin, which we need not specify now, and Q_s is the observable of the spin which is going to be measured. Let us assume that the interaction acts for a time T which is very large, and the interaction strength is constant and equal to 1/T for most of the time. The initial state |t=0> = |n>|f(r)> where f(r) is a wavepacket centered at position r, and |n> is a non-degenerate eigenstate of H_s.

We can divide the time T into N tiny intervals so that DelT=T/N. So the full wavefunction at the time T can be written as

|t=T> = [exp{-iDelT(p²/2m + H_s + pQ_s /T)} ]^N |t=0> Now the eigenstates of the spin-apparatus combine can be written as |p>|n'>, where |n'> are the modified spin eigenstates, and depend on the value of the momentum of the particle, p. These are the eigenstates of the instantaneous Hamiltonian. Using this the time evolution of the state can be expressed as |t=T> = Sum_p,m [exp{iE(p,m)NDelT)} |p>|m'><m'|n> <p|f(r)> where the energy eigenvalue E(p,m) is given by E(p,m) = p²/2m + p<m'|Q_s|m'>/T + <m'|H_s|m'> Now because the interaction is weak and slow, the states |m'> are nearly the same as |m>, and can be written as |m'> = |m> + O(1/T) + ... Similarly, the eigenvalues can be written in terms of |m> instead of |m'>: E(p,m) = p²/2m + p<m|Q_s|m>/T + <m|H_s|m> + O(1/T²) Now one can see that the second term in the above expression, being in the exponent in the time evolution of the state, with shift the position of a wave-packet by an amount <m|Q_s|m>: |t=T> = exp{-ip²/2mT-inT} |n>|f(r+<m|Q_s|m>)> But this is just the expectation value of the observable we started out to measure! This in essence is the idea behind protective measurement. The center of the wave-packet shifts by an amount equal to the expectation value of the operator being measured. The spin state on the other hand, does not change appreciably. So, in the limit T becoming really large, one gets the shift of the wave-packet, but the spin state remains the same, which means one has measured some observable of the spin without disturbing its state. It appears that we can know something about an unknown wavefunction, provided it is a non-degenerate eigenstate of the Hamiltonian.

Are there any problems?

In the last equation we only look at the effect of the interaction term on the wave-packet - we haven't looked at the effect of p²/2m. This term will make the wave-packet spread with time. And if the time is very large, as is the case here, the wave-packet will shift by a tiny amount, but may spread so much that we do not know where its center is.
Although the center of the wave-packet gets shifted, in order that an experimenter know how much is the shift, he or she would like to know where the center is located. A single measurement on the wave-packet can give the center to be anywhere within the spread of the wave-packet, and not necessarily at the true center.

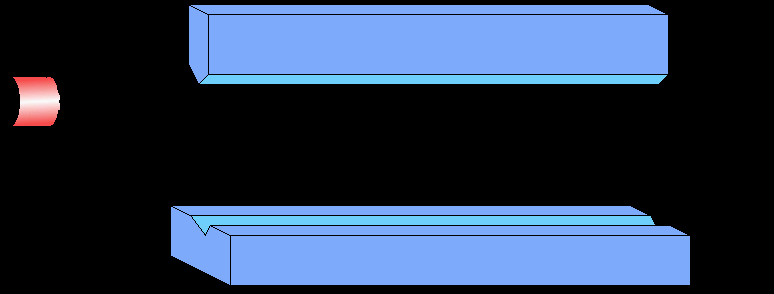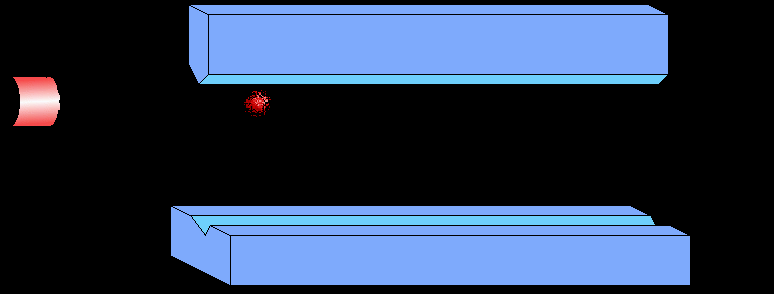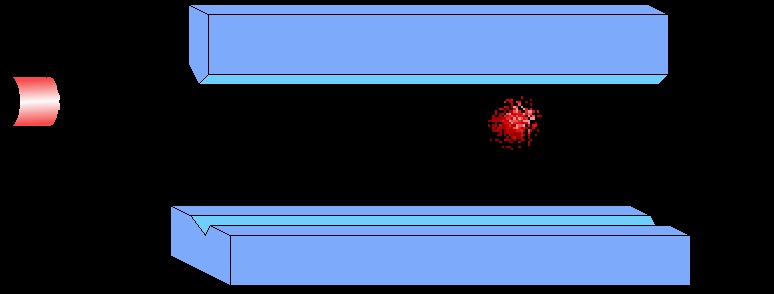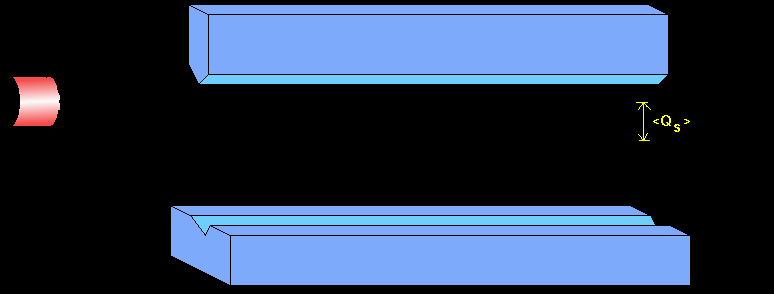
A schematic representation of a protective measurement. Here the postion wave-packet of the particle doesn't get entangled with the spin, hence the wave-packet doesn't split into two. The position of the wave-packet gets shifted by an amount equal to the expectation value of the observable being measured, that is <Q_s>. Notice how the wave-packet spreads a lot, and makes it difficult to measure the shift of the particle position.

This problem will be unavoidable when one tries to practically implement protective measurements. One might argue that the apparatus has to be of a classical nature, but here during the adiabatic interaction of the system and the apparatus the evolution of the apparatus has to be unitary. This whole analysis hinges on that. So, classical nature has to emerge later. It might emerge through interaction with some kind of an environment, by the mechanism of decoherence.

On the other hand one can treat the apparatus like a quantum system, as in the Stern-Gerlach experiment, and "detect" the apparatus using a classical apparatus. This will be a conventional measurement leading to a collapse of the apparatus wae-packet. In this scenario, we suggest two ways out of this problem.

Repeated measurement of a single state

A wave-packet, when detected, collapses to a random position within the spread of the packet.

One way is to make a large number of measurements on the same single quantum system. We can make use of the fact that in protective measurements, the wave-function of the system remains unchanged. After one measurement, if you detect the position of the wave-packet, you will get a particular random value within the spread of the packet. The system state remains the same, and so you can repeat the protective measurement which will give you another value for the position of the wave-packet. You can repeat this procedure as many time as you want. You can see that a large number of measurements will be like having an ensemble of the apparatus wave-packets. Detecting these wave-packets will then yield a large number of values, whose average will be the center of the wave-packet. This is a strange kind of a scenario where one uses a single quantum system, but an ensemble of apparatus!

Quantum Nondemolition Measurement of the Apparatus

There is another interesting way out of this problem. For this we make use of certain special kind of measurements, called Quantum Non-Demolition (QND) measurements. This scheme is based on repeated weak quantum nondemolition measurements performed on the apparatus. Recently Alter and Yamamoto analyzed the problem of a series of repeated weak QND measurement on a quantum system, to address the question of getting information about the unknown wave function of a single quantum system from such measurements. They concluded that it is possible to obtain the mean value of an observable in an unknown state, but no information can be obtained about the uncertainty of the observable. While the conclusions of Alter and Yamamoto were negative as far as using repeated weak QND measurements to determine the unknown wave function of a single system, it appears tailor-made to solve the problem of "reading the pointer position" in protective measurements. Thus we apply their scheme not to the system part of the protective measurement, but to the apparatus part instead. Then we can get information about the center of the wave packet, which in the protective measurement scheme carries information on the expectation values of observables in the system state.

A wave-packet going through a series of QND measurements.

The sequence of QND measurements evolves like this. With each measurement, the center of the wave-packet shifts slightly and also becomes slightly narrow. So, for a large number of such measurements, the center of the wave-packet executes a random walk around the original center, with progressively decreasing step size (see picture). In effect, the packet becomes narrower and narrower and comes closer to the original center as the number of measurements increases. It finally collapses on to the original center.

Thus one may proceed with a protective measurement by first allowing an adiabatic interaction of the system with an apparatus which can be treated quantum mechanically. This would result in a shifted wave packet of the pointer. One can then do a series of weak QND measurements on this wave packet to get the position of the center. This seems the most promising possibility for experimentally realizing protective measurements.

Does it really work for single system?

In a realistic situation, the time of interaction can only be very large, but not infinite. As a result, there is always a very tiny entanglement left, which is of the order 1/T. This entanglement does change the wavefunction to a tiny extent. In the unlucky situation the detection of the apparatus wave-packet might lead to a collapse to this infinitesimal, but non-zero, branch of the entangled wave-function.

Thus, if you are just given one single system in an unknown energy eigenstate, you cannot be hundred percent sure that you have measured the right state.

For a detailed analysis of protective measurements, see ( N.D. Haridass and T. Qureshi, quant-ph/9805012).

Back to my Physics Page